Art

I've always had an affection for procedural textures and image programming in general. Throughout my life I've programmed numerous systems, frameworks and programs to allow me to easily create textures, fractals and other interesting visualizations. Some of them are merely interesting, some could certainly be considered to be art and have actually been printed to decorate walls on a few occasions.

There are a few different things I experimented with - fractals (using replacement rules, complex number iterations (such as the Mandelbrot and Julia set) or just recursive rendering of primitive figures), procedural textures (usually based on noise functions such as Perlin Noise), GIF animations and actual videos. This part of the website is dedicated to all those things. Feel free to scroll down and simply browse the pictures if you're not interested in the details of their creation. Prepare for potentially high loading times though, a few of these images aren't particularly small. :)

Textures

Although texture generation turned out to be one of the topics I spent the most time working on throughout school and university, it's also the arguably least artful of these four categories - at least when it comes to the typical results (the work required to get there however requires way more creativity and skill than the other ones, so in that sense it's certainly more of an actual "art" which you have to perfect before achieving reasonable results). Consequently I won't spend too much time talking about procedural textures at this point and just give a few examples.

These were created with my very first self written image generation software back in 2008, hence the comparably low resolution. The individual textures were created using a set of prewritten generators (Perlin Noise, random noise, sine waves etc.), filters (negative, absolute, blur, contrast changes...) and operators (displace, add/substract/multiply, min/max) followed by one of several methods to colorize the generated grayscale image.

A few more recent examples can be seen below. I used different techniques and more advanced algorithms that would at times differ significantly from the original generator/filter/operator approach. I didn't focus that much on (noise) patterns and used explicit placement of lines and primitives instead that would result in more defined structures.

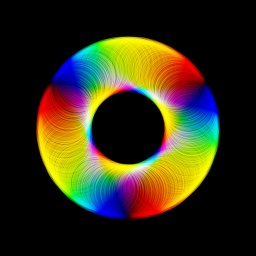
Fractals

So what is a fractal? After using the word for about ten times now I should probably explain very briefly. What better way to do that than quote wikipedia?

A fractal is a natural phenomenon or a mathematical set that exhibits a repeating pattern that displays at every scale. If the replication is exactly the same at every scale, it is called a self-similar pattern.

This extract from the article on fractals includes what we need to know - repeating pattern and self-similarity.
There are many different ways to generate fractals. One is the iterative solution of an equation in order to determine whether a complex number, when applied to a certain formular, converges or diverges. This is used for famous fractals such as the Mandelbrot or Julia set.

A different approach is recursively drawing primitive geometric structures. One of the more famous examples of this technique is the Sierpinski triangle: You start with one standing black triangle, then draw one inverted white triangle inside its center. Consequently there are 3 smaller black triangles and you continue applying this rule over and over again as demonstrated in this image.

Replacement rules work in a similar manner: You start off with a single line and define a rule by which this line is going to be replaced, usually by 2 or more shorter lines with the same start and end point. One of the most famous examples would be the Koch curve.

These systems however are immensely flexible and can yield an incredible variety of outcomes simply by varying the replacement rule. You can even use them to create the Sierpinski triangle or shapes resembling the julia set, although they are based on fundamentally different approaches of generation.
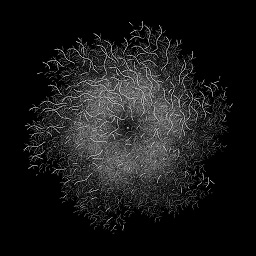
Below are a few examples of what I created using replacement rules.

One particularly interesting image is the one below showing a circular plot of the Koch curve while varying the recursion depth.

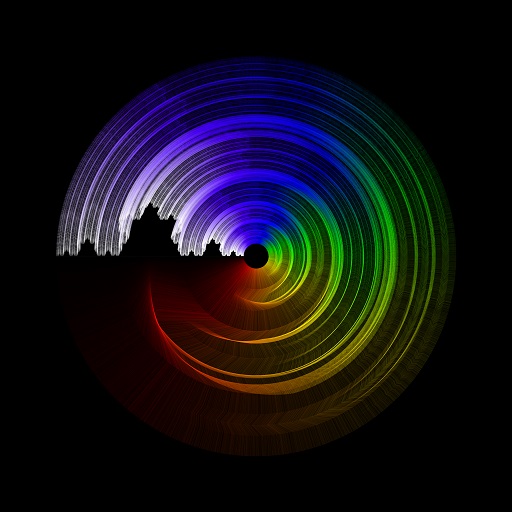
Generally coloring can add quite a lot to these pictures - quite literally an extra dimension. I experimented with several ways of coloring these fractals and ended up with a few promising results.

And that's about it when it comes to fractals for now. In case the images didn't make that perfectly clear already, please be aware that fractals are amazing. It's so stunning how a few ridiculously simple rules can result in these amazing structures with infinite details. If you'd like to see a few fractals in motion, make sure to stick around for the Videos part below.

GIF Animations

GIFs are animated images that can be displayed in any web browser and are hence much more accessible than actual videos. They come with a few limitations though - reduced color depth, no sound and ideally limited size, as huge GIFs will either take too long to load or won't be displayed at all. Consequently they are perfect for very short animations that loop over and over.
My personal interest in GIF creation awoke after browsing through the amazing variety of animations from Bees And Bombs. I started by doing "cover versions" of the author's work - basically just reconstructing a few of his animations to find out if I'd be able to achieve a similar level of quality.

Note: With some of these animations the aforementioned problem of browsers not replaying them might occur. If you'd still like to see them in motion, rightclick the respective image, click "Save Image", save it to your hard disk and open with any image viewing software of your choice that supports GIF playback.

Videos

While GIFs are fine for these smaller animations that take no more than a few seconds per cycle, there are certainly situations where actual videos come in handy. One of these cases is a non interactive way of parameter exploration. More specifically, varying the defining variables of a procedural texture or fractal over time and recording the whole process. This (quite literally) adds a whole new dimension to the world of fractals.

A good example of this concept is the following video of a sort of Pythagoras Tree where I applied sine based variations to the branches' scale factors and angles, resulting in constant mutations of the tree into various strange but interesting shapes.

Getting back to the replacement rules mentioned earlier, I then applied random variations to the node positions within the replacement rule over time and rendered the resulting fractals. It's truly amazing what peculiar shapes and structures emerge from one another in a matter of seconds.

Finally the following video demonstrates the systematic animation of a bunch of sine based "snakes". There's not much interesting math behind it and it's not even a proper fractal, but the video speaks for itself.

If you'd like to see more, make sure to check out the Youtube Channel. There are quite a few interesting videos covering parameter exploration on there, including "Birth of a Fractal" in which you can see a fractal grow seamlessly from its most basic replacement rule.

Photography

Last but not least a completely different topic. There's not that much to say about it either, so I'll just leave you with a bunch of pictures, some of which are more or less heavily edited in Photoshop.